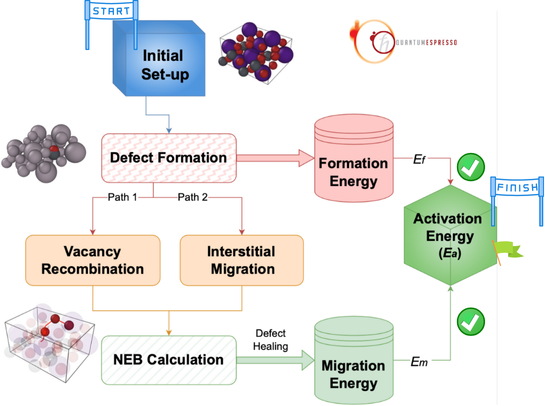
DFT Convergence Tips
Practical strategies for achieving convergence in challenging DFT calculations, including mixing schemes and initial guess optimization.
Read MoreSharing Knowledge & Life
Welcome to my blog where I share technical insights from my research and glimpses of life beyond the lab. From DFT calculations to table tennis strategies, this is where science meets personal interests.
Technical Tips & Tutorials
Getting Started with ML Force Fields
A beginner's guide to implementing machine learning force fields using ASE and MACE for molecular dynamics simulations.
Read More
Useful Quantum ESPRESSO Scripts
Collection of Python scripts for automating Quantum ESPRESSO workflows, from input generation to data analysis.
Read More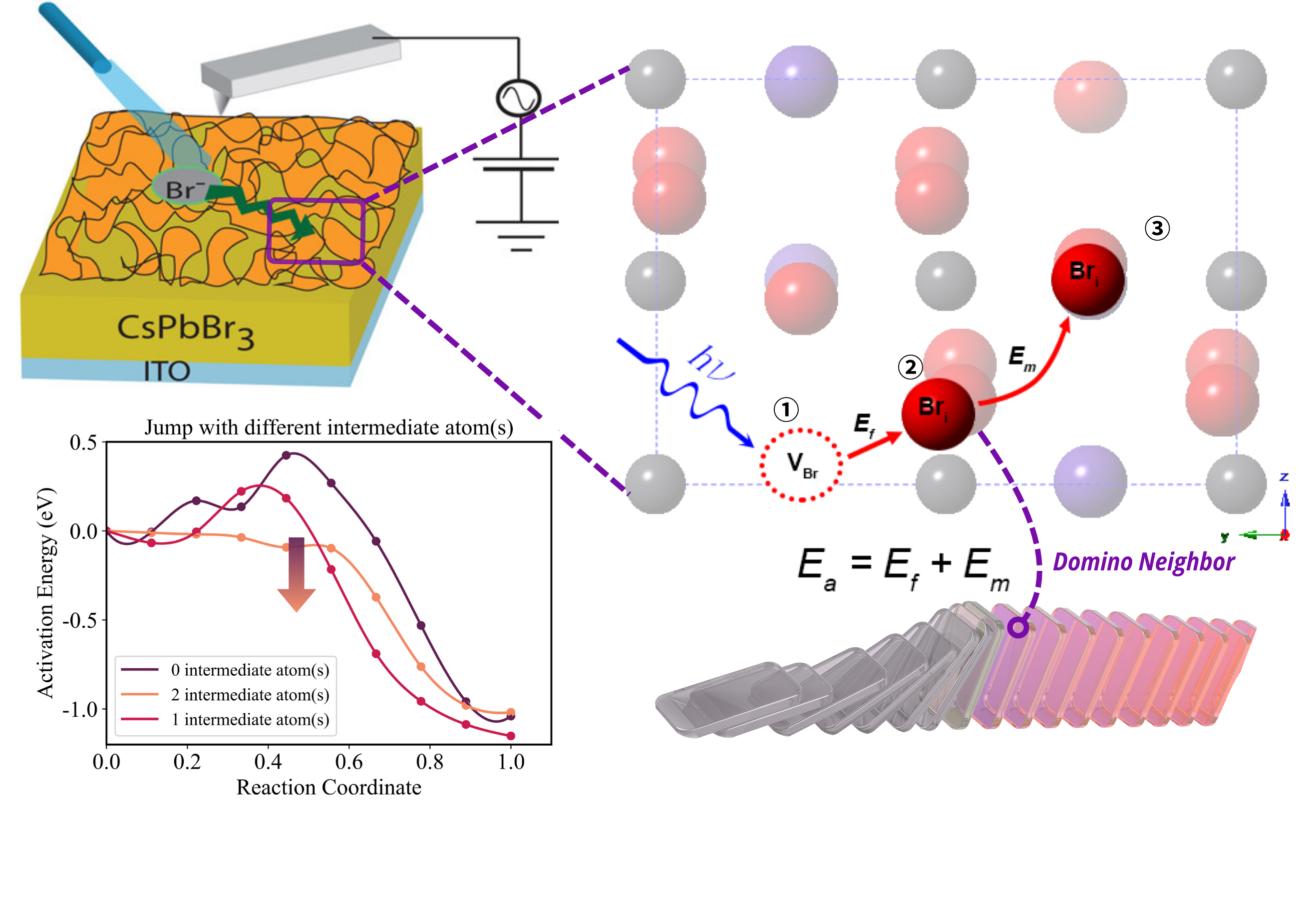
Beautiful Plots for Materials Science
Creating publication-quality figures for band structures, density of states, and crystal structures using matplotlib and plotly.
Read More2025 Yi Cao. This work is licensed under CC BY-NC-SA 4.0.
Life Beyond Research
My Table Tennis Journey
From beginner to competitive player - lessons learned on and off the table, and how sports complement research life.
Read More
Learning Tennis at 24
Why I decided to pick up tennis during my PhD and the surprising parallels between mastering a sport and research.
Read More
Four Seasons at Hopkins
Capturing the beauty of JHU's Homewood campus through the seasons - a photographer's perspective.
View Gallery
Conference Cities Through My Lens
Exploring DC, Boston, Bellevue, and beyond - combining conference attendance with street photography.
View GalleryQuick Code Snippets
Recent Snippets
Parse QE `relax.out` for energies
import re
from ase.io import read
# Read the last structure from Quantum ESPRESSO output
atoms = read('relax.out') # Automatically reads the last image
# Total energy in eV
energy_eV = atoms.get_potential_energy()
# Lattice parameters
cell = atoms.get_cell()
a, b, c = cell.lengths() # in Ångstrom
alpha, beta, gamma = cell.angles() # in degrees
# Print results
print(f"Total Energy: {energy_eV:.6f} eV")
print(f"Lattice Parameters (a, b, c): {a:.6f}, {b:.6f}, {c:.6f} Å")
print(f"Lattice Angles (α, β, γ): {alpha:.2f}°, {beta:.2f}°, {gamma:.2f}°")
return energiesPosted: January 10, 2025 | View on GitHub
Quick band gap extraction
import numpy as np
def extract_bandgap_from_qe_output(filename='bands.out'):
with open(filename, 'r') as f:
lines = f.readlines()
fermi_energy = None
band_energies = []
kpoints = []
current_kpoint_bands = []
for line in lines:
if 'the Fermi energy is' in line:
fermi_energy = float(line.split()[-2]) # in eV
elif 'k =' in line:
if current_kpoint_bands:
band_energies.append(current_kpoint_bands)
current_kpoint_bands = []
k_line = line.strip().split()
kpt = list(map(float, [k_line[2], k_line[3], k_line[4]]))
kpoints.append(kpt)
elif line.strip() and len(line.split()) == 2:
band_energy = float(line.split()[1])
current_kpoint_bands.append(band_energy)
if current_kpoint_bands:
band_energies.append(current_kpoint_bands)
# Convert to numpy array: shape (n_kpoints, n_bands)
band_energies = np.array(band_energies)
if fermi_energy is None:
raise ValueError("Fermi energy not found in file.")
# Shift energies relative to Fermi level
shifted_energies = band_energies - fermi_energy
# Find VBM and CBM
vbm = np.max(shifted_energies[shifted_energies <= 0])
cbm = np.min(shifted_energies[shifted_energies >= 0])
band_gap = cbm - vbm if cbm > vbm else 0.0
print(f"Fermi energy: {fermi_energy:.6f} eV")
print(f"Valence Band Maximum (VBM): {vbm:.6f} eV")
print(f"Conduction Band Minimum (CBM): {cbm:.6f} eV")
print(f"Band Gap: {band_gap:.6f} eV")
if band_gap == 0.0:
print("This material is metallic.")
else:
# Check direct vs indirect band gap
vbm_k = np.where(shifted_energies == vbm)[0][0]
cbm_k = np.where(shifted_energies == cbm)[0][0]
if vbm_k == cbm_k:
print("Direct band gap.")
else:
print("Indirect band gap.")
# Run it
extract_bandgap_from_qe_output('bands.out')
Posted: January 8, 2025 | Tags: Quantum ESPRESSO, ASE, band structure
2025 Yi Cao. This work is licensed under MIT License.
Stay Connected
Get updates when I post new content: